Relativistic Photon Moving with Velocity Greater than c

Libor Neumann

Prague, Czech Republic, email: LNeumann@chello.cz

The particular case is described where photon emitted from the moving light source is moving with the velocity greater than c in the stationary co-ordinate system. The photon velocity is dependent on the light source velocity. The velocity evaluation is strictly based on the special relativity theory transformation.

03.30.+p

Introduction

The paper title sounds like contradiction. The second relativity theory postulate is “Any ray of light moves in the “stationary” system of co-ordinates with determined velocity c, whether the ray be emitted by stationary or by moving body” [1]. Moreover the A. Einstein original paper includes the proof of the special relativity theory (SRT) transformation correspondence with the second postulate in §3.

Following text describes the particular case where properly used mathematical apparatus of SRT gives different result.

The following description uses definitions and symbols from §3 of SRT original description ¹. Two Cartesian co-ordinate systems (K - stationary system and k - moving one) are used. The stationary system K includes axes x,y,z and time t. Moving system k includes axes x,h,z and time t. The origin of the moving system moves with the velocity v (in x axis direction).

We use well known relativistic basic co-ordinate and time transformations described in §3 ¹

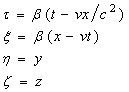
where

We use velocity transformation equations described in §5 ¹. General point or object moves with the velocity w (component and co-ordinate system is distinguished by index).

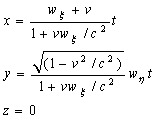
The time equivalence

SRT is based on the space co-ordinate transformation and on the time transformation. We look for the particular subset, where the time in stationary co-ordinate system K is equal to the time in moving co-ordinate system k. The analysis could be simpler if the subset exists.

(1)

We can solve equation (1). We can see; the plain orthogonal to the direction of the moving co-ordinate system velocity exists, where time in both co-ordinate systems is equivalent. We name the plain ET and we index the values connected with the plain by ET.

Let us analyse the features of the particular plain ET. We discover:

ET plain position computed in moving co-ordinate system k based on the same idea as above is described by (2) i.e. by the same equation with opposite sign as (1). It respects opposite orientation of the velocity v.

(2)

We can verify the relation between (1) and (2) by the standard relativistic co-ordinate transformation of any point at ET plain from stationary co-ordinate system K into moving co-ordinate system k (3) and vice versa.

(3)

We gain the same result as (2).

ET plain moves in both co-ordinate systems. The velocity of ET plain in stationary co-ordinate system K in x direction is x_ET/t. Using (1) we gain

By SRT velocity transformation of any point of ET plain velocity we gain

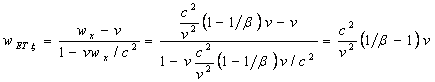
therefore

(4)

It looks like symmetry expected in SRT. We gain the same results from (2).

By the velocity transformation in orthogonal direction we gain equivalence 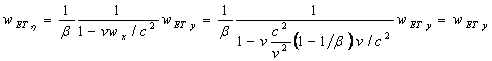(5).

(5)

We can describe the item c²/v² with use of the b definition from ¹ and gain (6).

(6)

Using (6) in (1) ET plain position can be described by (7).

(7)

We can see from (7) that ET plain is exactly in the middle of the distance between the origins of the co-ordinate systems only for b=1 i.e. only for v=0. The distance of ET plain from the stationary co-ordinate system K origin is greater than 0.5 vt for any v>0 (and t>0).

Measuring units

We know from basic course of physics that it is impossible to add or compare physical quantity without measuring unit knowledge and without conversion of all quantities into the common units. It is impossible to add distance in meters with distance in feet. SRT ¹ does not solve the question of the measuring units in detail.

The detail analysis of SRT transformations from the measuring unit point of view gives surprising result.

We can find that measuring unit of the y axis must be equal to the measuring unit of the h axis (due to equivalence of values and equivalence of distances). The same result we gain in case of the z and z axes.

Similar situation is in case of time measuring units at ET plain. The equivalence of time values (at ET plain) (1), equivalence of the velocity values in orthogonal direction (5) and equal measuring units of y,z and h,z axes imply the equal time measuring units in both co-ordinate systems (at ET plain).

Additionally we can define that the measuring units of x,y,z axes are equal (similarly to §3 ¹).

It is not possible to confirm the idea that the measuring unit of x axis is equal with the measuring unit of x axis as indirectly described in ¹.

Moreover obvious geometrical problem exists in case of this interpretation.

Figure1 - Distances between co-ordinate systems origins and ET plain

Let us compare the sum of distances of ET plain from the co-ordinate systems origins with the distance between the origins. From the geometry we know, that the sum of distance between the origin of the stationary co-ordinate system K and ET plain and the distance of the same plain from the origin of the moving co-ordinate system k must be equal to the distance between the origins.

The distance D between origins is from the definition in §3 ¹

The same distance is described by (8) evaluated from (1), (2) (using (6)).

(8)

We can see from (8), that equivalence of distances can be valid only in case b=1 i.e. v=0 (if we consider the equal measuring units in both co-ordinate systems).

It means, if we consider the equal measuring units of x axis and x axis, SRT transformation can be valid only for v=0 (due to the geometrical reasons connected with the co-ordinate systems origins displacement). It gives no physical sense.

We can try to solve the problem by discovering the ratio between measuring units of the x and x axes.

We can suppose the ratio between measuring units of x and x axes is a. We know from (1),(2), and (4) that the original and transformed relations give the same values (with opposite signs). We can describe the distance geometry with respect of measuring unit ratio by (9)

(9)

We can see from (9) that it is possible to describe distance D equal vt as sum the same values together with the fact that distance of ET plain can be greater than 0.5 vt in co-ordinate system K by the proper selection of the measuring unit ratio.

We can compare (7) with (9). We can see that the geometrical problem of SRT transformation can be solved only if the ratio of measuring units of x and x axes is b.

It means, the physical length unit used for the distance description at x axis is b-times smaller than the length unit at the all other axes (x,y,z,h,z). The same is valid for the velocity measuring units. We will identify the velocity unit at the x,y,z,h,z axes by [U] and the velocity unit at the x axis [u] in the following text.

Photon

Let us have the light source moving with velocity v in direction of x axis. It is placed in the origin of the moving co-ordinate system k as usual in SRT. Both co-ordinate systems origins are equal at t=t=0. The light source emits photon P at t=t=0 with the velocity c (measured in units [U]) in the direction that photon moves in ET plain in direction of h (y) axis. Photon moves in x axis direction with the velocity (10) measured in [u] – measuring unit of x axis.

(10)

The photon velocity x component is equal to ET plain velocity (2) (using (6)). Photon P moves with the velocity (11) in x axis direction - measured in the units [U].

(11)

We can calculate the photon orthogonal velocity component in the h axis direction (12) (measured in [U]) i.e. the photon P velocity in ET plain.

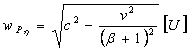(12)

We know all photon P velocity components in moving co-ordinate system k (w_P_z=0). We can transform photon P movement into the stationary co-ordinate system K by standard SRT velocity transformation with respect of the measuring units.

We can use previously described transformation equations (4) and (5) (valid at ET plain)[a].

We gain (13) and (14) (both in [U]).

(13)

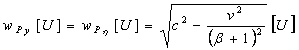(14)

We can compute photon P total velocity w_P in the stationary co-ordinate system K (15) in units [U] i.e. in the same measuring unit as photon emission velocity c is described.

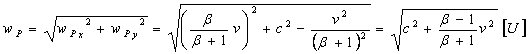(15)

We can evaluate (15) using (6) and gain 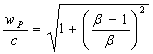(16).

(16)

We can see directly from (16) (no measuring unit) that photon P emitted from the moving light source is moving with velocity grater than c in stationary co-ordinate system for any b>1 i.e. for any v>0 (and t>0). We can see from (16) that the photon P velocity is dependent on the light source velocity v.

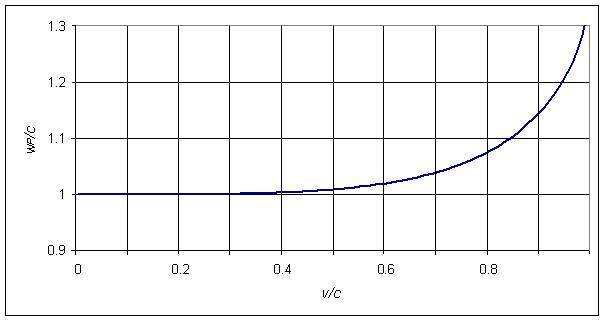
Figure 2 - Graphical representation of the photon P total velocity w_P dependence on the light source velocity v.

Conclusion

Described particular case shows the existence of at least one situation where photon emitted from the moving light source moves with velocity grater than c in the stationary co-ordinate system and the photon velocity is dependent on the light source velocity. The calculation is based on the correct use of SRT transformation including measuring unit conversion. The result is in direct contradiction with the second relativity theory postulate.

It must be noted, that the variant of the equal measuring units at all space axes can be taken into account. The geometrical distance inconsistency of SRT transformation described above exists in the particular case.

It means that at least one particular situation exists where SRT is internally inconsistent.

The particular case shows, that the proof described in §3 ¹ can not be generally valid. The existence of the particular case proves that the second relativity theory postulate is mathematically unsupported by SRT transformation.

[a] Equation (4) uses [u] and [U] units and (5) uses only [U] units. We must substitute velocity described in [u] units into (4) i.e. (10) to receive result in [U]. We must substitute velocity in [U] units into (5) i.e. (12) to receive results in [U].