Late analysis results of the paper “On the electrodynamics of moving bodies“ – kinematical part

 

 

 

Libor Neumann

 

Prague, Czech Republic

 

LNeumann@chello.cz

 

Abstract

The paper presents analysis results of the original text of special relativity theory. The paper shows that the proof of the length contraction is incomplete. The velocity equations and the proof of the light velocity invariance were misinterpreted.   The coordinate axes are not orthogonal and no origin translation exists in time-space. The validity space of the transformation is moving plane in classical three-dimensional space. The mathematically valid transformation does not support relativistic effects. There is no possibility to fulfil all necessary physical features of the relativity transformation together from the mathematical point of view.  The serious physical use of the transformations is excluded.

 

PACS: 03.30.+p

1           Introduction

The paper “On the Electrodynamics of Moving Bodies” (EMB) was published more 100 years ago [1]. The original EMB paper was not peer reviewed before publication.

Are the ideas of the special relativity theory valid or not? It is not clear yet.

The EMB paper is the background of the specific field of modern physics. Many papers are based on the ideas described in the EMB text. Many papers are dealing with the relativity and directly or indirectly use the ideas of the EMB text.

General relativity [2] is directly based on the EMB conclusions. Relativity theory is an ordinary part of physical courses and scientific research.

The papers and the discussions impeaching validity of the special relativity still exist [3, 4, 5] on the other site.

Two groups of experts exist. One majority group believes in correspondence of the EMB ideas with real world. The other group believes in the opposite.

Some measurable effects exist which can be interpreted as the indirect prove of EMB validity. The effect could be explained the different way as well. Existence and validity of a different explanation of the effects was not disproved.  No direct generally accepted experimental proof of EMB validity exists. Many attempts were made; many teams were working in many scientific projects focused to the direct proof of relativity theory. None was successful yet. Remember the experiments with travelling atomic clocks [6] or the gravity waves detection experiments [7] as examples. Many experiments are interpreted as an experimental proof of special relativity theory by one group of experts and the other experts disagree with the interpretation. 

Results of my gravity measurements [8] can be interpreted as disproving of general relativity theory. It was the reason I had made a decision to try to find the place where a mistake could be. 

It was the reason for my analysis. I made the decision to start from the roots, from the original EMB paper. I tried to understand special relativity theory in detail. I started the analysis of the EMB.

The analysis results surprised me. They are very different from everything I read. It was the reason for publishing the analysis result.

 

The results of the analysis are described in form of questions, answers and explanations to enable understandable description of the main topics and respect the paper size. The analysis deals with the kinematical part of the EMB text.

 

The explanations refer many times to specific parts of the original EMB paper. The selected parts of original EMB paper are used in the explanations with unique identifiers. The identifiers EMBxx (where xx is unique number) are used.

2           Questions and answers

Question 1:  Does EMB text prove length contraction?

Answer 1:  No. The proof in §4 is incomplete.

Explanation 1

 

Question 2: Does the place in moving coordinate system exist where the time is equal to the time in stationary coordinate system?

Answer 2: Yes. The moving plane exists where the time is equal in both coordinate systems.

Explanation 2

 

Question 3: Why the results of the sphere transformations are different in case of light velocity limit proof in §3 and length contraction proof in §4?

Answer 3: The transformation in §3 includes the time transformation but the transformation in §4 does not.

Explanation 3

 

Question 4:  Does velocity equations in §5 describe composition of velocities?

Answer 4:  No. The equations describe transformation of velocities?

Explanation 4

 

Question 5:  Does proof of light velocity limit in §3 correspond with EMB light velocity invariance postulate described in §2? 

Answer 5:  No. The proof describes two different physical effects. No proof of light velocity invariance is described in EMB.

Explanation 5

 

Question 6:  Is transformed coordinate system translated relatively to original one.

Answer 6:  Yes and no.

In case of time-space coordinate systems (4 dimensions) both coordinate systems have the same origin for any time.

In case of classical space coordinate systems (3 dimensions) the coordinate systems origins are translated. The distance is time dependent.

Explanation 6

 

Question 7:  Are coordinate axes orthogonal in transformed coordinate system?

Answer 7:  Yes and no.

In case of time-space coordinate systems (4 dimensions) time and one space axes are not orthogonal.

In case of classical space coordinate systems (3 dimensions) all coordinate axes are orthogonal.

Explanation 7

 

Question 8:  What is the validity space of the EMB transformation with orthogonal axes and translated origins?

Answer 8:  It is moving plane orthogonal to the moving direction. The EMB (relativistic) transformation is equal to Galileo transformation in the plane. No relativistic effect exists in the plane.

Explanation 8

 

3           Explanations

3.1         Explanation 1

The EMB text in §4 (EMB12) includes the statement that the equation (EMB11) describes the ellipsoid of revolution without any proof.  The statement must be valid in the coordinate system, where (EMB10) is equation of the sphere. In our case it must be valid only in the coordinate system k (EMB2). The equation (EMB11) need not describe the ellipsoid in the coordinate system K. It must be proved if the EMB statement is true or false.

 

It is not generally true that the same geometrical configuration is described by the same equation in any coordinate system. It is impossible to declare that the equation of the ellipsoid in one coordinate system must be the equation of the ellipsoid in second coordinate system. We can illustrate it in the following example. The equation x=const. can be the equation of a line in the Cartesian coordinate system if x is one of the coordinate axes. The same equation x=const. can be the equation of a circle in the cylindrical coordinate system, if x is distance from the origin.

 

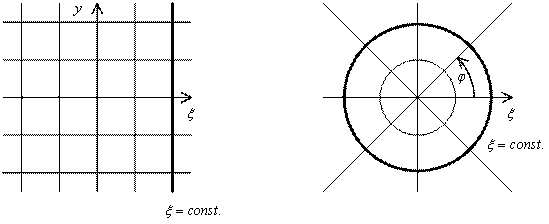
Figure 1. The example of the different geometric shapes of the same equation in the different coordinate systems.  The Cartesian coordinate system is on the left. The cylindrical coordinate system is on the right.

 

We can imagine the specific transformation mapping one Cartesian coordinate system with three coordinates measured in meters into the second Cartesian system where two axes are measured in meters and third axis is measured in feet. The similar transformation equation to (EMB9) describes the transformation in this case (without the time transformation – see Explanation 7). We can imagine using of the same procedure as described in EMB in §4 for our case.  This procedure gives the same results, i.e. the sphere equation is transformed into “ellipsoid” equation.  We know from experience that the transformation does not change the real sphere. The sphere is unchanged, but the equation describing the same sphere in the second coordinate system is different from the equation in the first coordinate system.

 

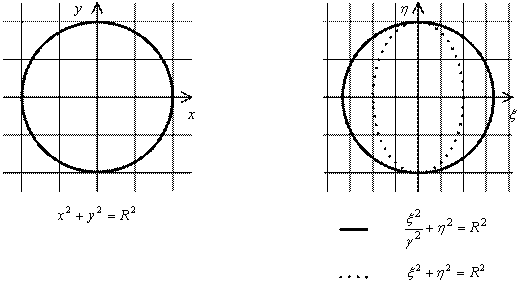
Figure 2. The example of the circle transformation with the scale change in one axis.  The scale of the coorinare axis x is γ times smaller than the scale of the coordinate axes x, y, h. The original circle on the left is transformed into the circle on the right. The equation on the left looks like the equation of the circle and it describes the circle. The equation on the right looks like the equation of the ellipse and describes the circle (the solid line).  Another equation on the right looks like the equation of the circle and it describes the ellipse (the dotted line).

 

It is not possible to tell what geometrical configuration is described by the equation in the specific coordinate system without the knowledge of the coordinate system features. The isolated equation cannot be used for any statement dealing with the geometrical configuration.

 

Q&A

3.2         Explanation 2

We suppose for the analysis that the time scales in both coordinate systems are equal. We find the answer from (EMB9) where we set  i.e. . We get

by modification. The approximation x = vt/2 of the equation

is useable for the small values of v/c. The error is smaller than 7% for v/c<0.5.

 

This implies; the situation t=t exists in the plane perpendicular to the x axis moving with the velocity approximately v/2 in the stationary coordinate system. The plane moves with the velocity approximately –v/2 in the moving coordinate system. It is approximately at the halfway between the origins of both coordinate systems.

The time relations in both coordinate systems are t>t for all points with the x (x) coordinate smaller than the plane position and t<t for all points with the x (x) coordinate greater than the plane one.  Therefore the event exists (at t>0) for any point with constant x >0 when the transformed time is equal to the original one. Before this event the transformed time is smaller than the original one and after the event it is up side down. The similar effect exists in the moving coordinate system for x<0.

The transformed time at the origin of the moving coordinate system k is t<t. It agrees with known equation (EMB13) for all positive times.

Transformed time at the origin of the stationary coordinate system K is t>t. It is the opposite situation. The equation (EMB13) is not valid there.  It results from (EMB9) for the origin of the stationary coordinate system where t=bt, so

i.e. the opposite situation to the “time dilatation”.

We can see that t=t is valid at the origins of the coordinate systems only at t=t=0. The time transformation features of EMB transformation are equivalent with the different time scales of the clocks in different places.

 

Q&A

3.3         Explanation 3

The spherical wave and the result of transformation of the spherical wave in §3 are described

 (EMB5)

 (EMB6)

The sphere surface and the result of transformation of the sphere surface in §4 are described

 (EMB10)

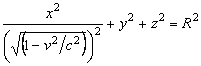 (EMB11)

The equations in §4 should be valid in any tome, the equations in §3 should describe spheres in any selected time.

We return to the EMB text §4 describing the sphere and the ellipsoid. The time is defined in the coordinate system K (EMB2) at the every point on the surface described by equation (EMB11). It is valid for t=0 and x≠0 that t≠0 according to (EMB9). The points where x≠0 exist on the surface described by (EMB10), therefore t≠0 must be valid at those points in the coordinate system k.  The points where x=0 exist on the surface, therefore the points where t=0 exist too.  It means the equation (EMB10) describes the set of points existing at the different times t. The equation (EMB10) can not describe the solid sphere at the specific time in the coordinate system k. Every time difference causes distance difference between the stationary and moving coordinate systems.

We can find in the equation (EMB11) deduction from (EMB10) that the equation for the time transformation (EMB9) is not used. The definition t=0 in (EMB11) is not transformed. The time transformation is omitted without any valid reason.

This is the basic difference from the transformation of (EMB5) into (EMB6). The time transformation is used in this case.  Unused time transformation is the cause of the different results of those two sphere transformations.

 

Q&A

3.4         Explanation 4

In the following text we suppose that relations (EMB14) describe velocity composition in one specific coordinate system (not transformation between two coordinate systems). We will solve the composition problem of two orthogonal velocities. We have two orthogonal velocities v and w in one coordinate system.

We will analyse two different compositions with the different sequence of the velocities. The first composition is named I and it is based on the reference velocity v. It can be described symbolically as v+w. The second composition is named II and it is based on the reference velocity w. It can be symbolically described as w+v.

 

The case I. We orient the coordinate system in the parallel way with the reference velocity v as usual in the EMB text. The velocity components of both velocities are in this case vx=v, vh=0, wx=0, wh=w. We gain from (EMB14) and (EMB15)

 

The case II. We orient the coordinate system in the parallel way with the reference velocity w. The velocity components of both velocities are in this case vx=0, vh=-v, wx=w, wh=0. We gain from (EMB14) and (EMB15)

We can see from both cases that the composed velocity magnitude is equal in both cases.  The magnitude is different than the velocity magnitude of the composed velocities based on Euclidean composition of distances divided by the time interval.

The specific velocity component magnitudes are different in both cases.  The composed velocity component in the v velocity direction is greater in the case I than in the case II.  By contrast the composed velocity component in the w velocity direction is smaller in the case I than in the case II.  The direction of composed velocities must be different in both cases.

It is interesting that the composition of orthogonal velocities changes the magnitude of orthogonal component of the composed velocity.

Figure 3. Two results of the velocity composition. Vector I describes the v+w EMB velocity composition result (case I). Vector II describes w+v EMB velocity composition result (case II).  The dotted vector E describes the velocity composition result v+w and w+v based on Euclidean distance composition and the velocity definition.

 

We see that the equations (EMB14) describe vector operation which is not commutative. The result of the operation is dependent on the vector sequence.  This feature is not acceptable in the velocity composition in physics.

 

Let us test a hypothesis that (EMB14) describe velocity transformation between two coordinate systems k and K.

The point position transformation equation (EMB9) and the velocity transformation equation (EMB14) can not be independent, if they are used for the transformation in physics. The relations between the position transformation and the velocity transformation must be independent on the sequence of the transformation and the differentiation. The result must be the same if we count the velocity first by the differentiation and transform the velocity or if we transform the positions and time first and then count the velocity. It can be described by the equation

,

where Tp is the position transformation, Tv is the velocity transformation and x is the position of a point.

Let us deduce the equations for Tv from (EMB9) and compare the result with the EMB velocity equation (EMB14).

 

We are working in the inertial system, in system with the constant velocities. We can use differences for simplicity. We deduce the velocity transformation per components (with respect of the transformation direction).

We gather the velocity transformation directly deduced from (EMB9) is equal to (EMB14) (the opposite transformation direction is reflected by the sign change of the coordinate system velocity v as used in the EMB text). The velocity equation (EMB14) corresponds to the position transformation (EMB9) as usual in physics.

 

The result implies that interpretation in the EMB text describing equations (EMB14) and others in §5 as the velocity composition in one coordinate system is wrong. The statements in (EMB16) and (EMB17) text can be valid only for transformation into the moving coordinate system.

 

Q&A

3.5         Explanation 5

The text EMB in §3 describes the equation (EMB6) as result of the (EMB5) transformation. It is described as a proof of the EMB transformation correspondence with the light velocity invariance postulate (EMB1).

 (EMB5)

 (EMB6)

The equation (EMB5) is interpreted as the equation describing the spherical wave propagated with the velocity c in the coordinate system K.  The equation can describe the parametric sphere with the centre at the origin of the coordinate system K. The equation can describe the wave propagated from t=0 with the velocity c.

The equation (EMB6) is interpreted similar way. It is interpreted as the equation describing the spherical wave propagated with the velocity c in the coordinate system k.  The equation can describe the wave propagated from t=0 with the velocity c. It is interpreted in EMB as the proof of the light velocity invariance.

 

Let us analyse the proof in more detail.

Equation (EMB5) describes the parametric set of the spheres with the radius c.t and with the centre at the origin of the coordinate system K in the Cartesian coordinate system K with the axes x,y,z.  The equation can be used for description of the spherical wave propagated with the velocity c.

It is not sure if the equation (EMB6) describes parametric set of the spheres in coordinate system k. The EMB text does not contain any proof of this interpretation of (EMB6). It is not possible to deduce from the same mathematical form that the described geometrical entity is the same. It is well known fact (see Explanation 1).

 

Let us assume existence of the proof. In this case the equation (EMB6) describes the parametric set of the spheres in the coordinate system k with the axes x,h,z with the radius c.t and with the centre at the origin of the coordinate system k.

Let us determine how is one sphere with the radius c.t in the coordinate system K transformed into the coordinate system k. What is the radius of the transformed sphere?  If the spheres have the same radiuses R=c.t=c.t=r in both coordinate systems and the light velocity c is the same in both coordinate systems, it must be valid t=t at every point of the sphere surface.

If we suppose the spherical wave, the equation t=t must be valid for all t and all t at any point of the sphere.  The set of those points is whole space. It is in the contradiction with the analysed features of the time transformation (EMB9) analysed in the Explanation 2. We know that the equation t=t  is valid only in the plane perpendicular to the moving coordinate system velocity direction at approximately half of the distance between the coordinate systems origins. It is valid t≠t at all other positions. We have two possibilities:

  

Let us look at the sphere centres.  Every sphere from the set of spheres included in propagated spherical wave in the coordinate system K has the centre at the origin of the coordinate system K according to (EMB5).  Every sphere from the set of spheres (if they are spheres) included in propagated spherical wave in the coordinate system k has the centre at the origin of the coordinate system k according to (EMB6).  The origin of the coordinate system K is equal to the origin of the coordinate system k only at the time t=t=0 as usual in EMB. The centre of the transformed sphere is at the other place than the centre of the original one at any other time. The spheres can not be identical. The spheres must have the different centres moving each other with the velocity v.

Let us note the equation describing the transformed spherical wave or the sphere with the centre at the origin of the coordinate system K  (EMB2) can be described in the Cartesian coordinate system k by equation

or if we consider the scale transformation in x,t axes (see Explanation 6 and Explanation 1) the equation could be

.

Compare it with (EMB6).

 

We summarize.  Equations (EMB5) and (EMB6) do not describe the same physical effect and they do not prove the light velocity invariance of the transformations described in EMB. No other proof of the light velocity invariance is described in EMB.

 

Q&A

3.6         Explanation 6

Let us analyze the EMB transformations from mathematical point of view.

We will analyse the transformations described in the EMB text as a vector transformation.

The mathematic area dealing with vector transformation is part of linear algebra (vector algebra, tensor algebra). We can read in linear algebra textbooks, that the basis of the coordinate system and the origins are essential part of the transformation. We can read [9 – chapter 3.4, chapter 5.1], [10], [11], [12] that the coordinate transformation is unambiguously related with the coordinate systems bases and origin shift.

General vector space (geometry) transformation consists of origin shift (translation) and change of basis [13]. Translation can be described by translation matrix (1) [14].

                  (1)

 

General transformation can be described by general transformation matrix (2) [15]

                    (2)

 

Where a is basis change matrix and T is translation vector in result coordinate system.

We will use EMB notation where coordinates in the original coordinate system K are x,y,z and coordinates in the result coordinate system k are x,h,z.  

3.6.1        4D – time-space

We can formulate a 4D hypothesis. It is possible to do it. Some parts of EMB text can be understand this way (EMB3), (EMB4), (EMB9). The point in our 4D space is an event.

General transformation in 4D space can be described by general transformation matrix

 

We can write directly from (EMB9) the transformation matrix b in general transformation matrix form

 

                       (3)

We can see that the (EMB9) transformation includes zero translation vector T.  The transformation includes only bases change. The (EMB9) transformation in 4D space does not shift the coordinate system origins.

3.6.2        3D – classical space

The EMB text (EMB2) describes clocks “be in all respects alike”.  It can be understand from the mathematical point of view as both 3D coordinate systems are parameterized by the time attribute at any point. The note “this “t” always denotes a time in stationary system” can be understand as the attribute of the stationary coordinate system is named “t”. The value of the attributes t and t at different points is referred to the EMB §1 text.

We can write directly from (EMB9) the transformation matrix b in general transformation matrix form

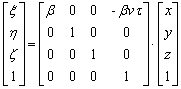                         (4)

 

We can see that the (EMB9) transformation in 3D space includes nonzero translation. It is not simple translation. The transformation includes bases change as well (compare with (1) and (2)).

 

Q&A

3.7         Explanation 7

3.7.1        4D – time-space

Let us find the inverse mapping to (EMB9). We solve inverse matrix c=b-1 (3).  We need determinant det(b).  We calculate det(b)=b2(1-v2/c2)=1.  Determinant is sometimes called scale factor for volume. We see that the (EMB9) transformation in 4D space does not change scale of volume because det(b)=1 (for v<c).

Inverse matrix c is

We can write from the inverse matrix c

x=bvt+bx=b(x+vt) and t=bt+bvx/c2=b(t+vx/c2).

The inverse matrix c in 4D space gives the same results as the EMB text in (EMB7) and (EMB8).

 

Let us verify if all bases vectors are orthogonal.

We can describe unit vectors of the coordinate system k base in coordinate system K from inverse matrix c

et=(b, bv,0,0), ex=(bv/c2,b, 0,0), eh=(0,0,1,0), ez=(0,0,0,1)

The unit vector lengths are

 

We compute dot products of every pair of unit vectors. We find out that all dot products but one is zero.  Every base vectors but one pair are orthogonal. The exception is et and ex.

et . ex=b2v/c2+b2v=b2v(1+1/c2)

 

We can make general 4D space conclusions:

 

We note the 4D space we are using is not metric space. It is affine space. It is not possible to measure the distances or the angles in this space. The value of the dot product ex . et has no physical meaning in affine space (the same is valid for the unit vector length).  Zero value is important for perpendicularity test. It is possible to test perpendicularity in our case.

We can change our space into the metric space for better clearness. We can multiply both “time” axes t and t by any velocity v0. We gain the metric space. We can measure the distances and the angles in that space. We get in this case

et . ex=b2vv0/c2+b2v/v0=b2v(1/v0+ v0/c2)

and we can measure the angle between the x and v0t axes (between the ex and et  basis vectors). It is

.

We can see the angle is dependent on the ratio v/v0 and on the ratio v/c. We get

for v=v0=c.  It means that the x and v0t axes are parallel in this case. The 4D space is reduced into the 3D space with one “integrated space-time axis” plus the two standard space axes in this case.  

 

Figure 4. The schematic drawing of the 4D EMB transformation. Only the two dimensions are shown in the figure.  The unit vectors of the both coordinate systems K and k, coordinate axes and the three points P1, P2 and P3 describing the three different events in the coordinate system K are drawn.  The points P1 and P3 describe position of the stationary mass point at the different time moments.  The points P1 and P2 describe the two synchronous events at the two different localities.  The coordinates in the coordinate systems K and k are drawn. We can see if the mass point is stationary in the coordinate system K, the coordinate x decreases its value and the coordinate t increases its value in the coordinate system k with the growing time t.  The two synchronous events have the different coordinate value t in the coordinate system k.  We can see from the figure that the coordinate value x in the coordinate system K is different from the coordinate value x in the coordinate system k. We can see the decreasing coordinate value t with the increasing coordinate value x for the synchronous events.

3.7.2        3D – classical space

We name the distance of the coordinate systems K and k origins in the coordinate system K as DK and the same distance in the coordinate system k as Dk.

The transformation matrix b in general transformation matrix form is (4) where -bvt=Dk.

Let us find the inverse mapping to (EMB9). We solve inverse matrix c=b-1.  We need determinant det(b).  We calculate det(b)=b. We see that the (EMB9) transformation in 3D space changes scale of volume because det(b)≠1 (for v>0) (compare with Explanation 1).

Inverse matrix c is

 

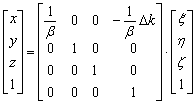
We can write from the inverse matrix c

x=x/b+DK= x/b-Dk/b,

where DK=-Dk/b=vt and from the original matrix b

x=bx+Dk=bx-bDK.

 

Let us verify if all base vectors are orthogonal.

We can describe unit vectors of the coordinate system k base in coordinate system K from inverse matrix c

ex=(1/b, 0,0), eh=(0,1,0), ez=(0,0,1).

The unit vector lengths are

 

We compute dot products of every pair of unit vectors of the coordinate system k base. We find out that all dot products are zero.  Every base vectors pair of coordinate system k is orthogonal. Every base vector in 3D space is orthogonal to every other.

 

We can make the first 3D space general conclusions:

 

Q&A

3.8         Explanation 8

We are in classical 3D space (see Explanation 6 and Explanation 7). EMB transformation works with t and t attributes. Both can be supposed as attributes of every point in the 3D space. The equation t=b(t-vx/c2) from (EMB9) can be interpreted as relation between both attributes.

We analyse dependency of the origins translation on the t attribute value.

We find from DK and Dk definition and from translation definition applied to the (EMB9) the relation DK=vt (in coordinate system K). It implies directly that exists only one value of the t attribute for every specific DK or Dk.  It implies directly, that every point in the space has to have the same value of its t attribute (only one translation exists for every point in the space – see translation definition [14]).

We can write direct and inverse transformation

x=bx-bDK=bx-bvt=b(x-vt)

x=x/b+DK= x/b+vt

 

Let us note different scales in both coordinate systems.

We can see that our inverse transformation equation is different from the equations (EMB7) and (EMB8). Inverse mapping does not include t variable as in EMB text.

 

We have additional general conclusions:

 

Let us analyse transformation features linked with the t attribute. We use the relation between both attributes t=b(t-vx/c2) from (EMB9). The relation t=b(t-vx/c2) describes slant line where t value decreases with increasing x. We know that the t value has to be constant with respect of x. Therefore we always can find the specific coordinate x where the relation is valid for any t value independently on t value (if v>0).  It means, we can select any t  value independently on t value and use it in inverse transformation even in the product vkt (the k index distinguishes the vk constant value in the coordinate system k linked with t attribute from the v constant value linked with the t attribute in the original coordinate system K).

It implies; there exists that x where the product vkt  has any value independently on the t attribute value.

If the product vkt is the coordinate system translation in coordinate system k as described in (EMB7), it has to be only one specific distance valid in whole validity scale of the transformation. It means thet attribute has to have only one specific value in the inverse transformation validity scope if vk is constant.

There exists only one value of x coordinate where thet attribute has the specific value. The value of thet attribute has to be different at any other point with the different x (x) coordinate.  Therefore the inverse translation dependent on the t attribute is valid only in the plane perpendicular to the x (x) axis.

 

Let us find the position of the plane. We know from the distance between origins comparison in different coordinate systems Dk=bDK (scale change must be applied to the distance description in different coordinate systems), then

vkt=Dk=bDK=bvt.

We gain the inverse translation validity condition

t =btv/vk.

The inverse translation has to fulfil two conditions dealing with the relation between t and t in its validity scope i.e. relation

t =b(t-vx/c2)

and the condition

t=btv/vk.

We solve the position where both equations are valid

btv/vk = t = b(t-vx/c2).

The solution is

x=tc2(1/v-1/vk).

We see that the plane position is dependent on the t attribute value (i.e. on the distance between the origins) and on the relation of both constants v and vk.  We can choose the ratio a=t/t=bv/vk.  The plane position can be described

.

We get general inverse transformation

x = x/b+ vt = x/b+ vk t/b=x/b+ vt/a.             (5)

 

We gain a=b, x=0 and t=bt for v=vk. The inverse transformation is

x = x/b+ vk t /b = x/b+ vt/b.

We gain a=1, vk=bv and

for t=t. The inverse transformation is

 x = x/b+ vk t/b = x/b+ vt.

We have infinite number of choices to select a (relation between v and vk i.e. relation between t and t).

All selections are equivalent from mathematical point of view.

 

We have additional specific conclusions valid in the case of using the t attribute in inverse transformation:

 

We can see the situation for t=t i.e. a=1on the figure 5.

Figure 5. Schematic drawing of the validity scope of 3D EMB transformation. Only one coordinate system dimension and the t and t attribute value are shown on the figure.  Coordinate system k at time t1 is drawn in the coordinate system K. The coordinate system k origin 0k is placed at position vt1 (measured in coordinate system K scale). The plane P1 is placed perpendicularly to the x (x) axis (it is drawn as a point – axes y and z is not drawn in the figure). It is valid t1=t1 in the plane P1.

 

We can analyse relativistic effects in the 3D space transformation validity scope (in the plane) for t=at where a is chosen constant:

into velocity transformation equation (in the y (h) direction) (EMB14)

.

 

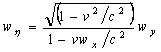We gain

.

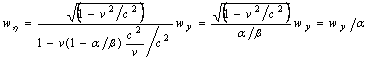We can see identity. No velocity limit exists in the plane. The velocity transformation includes only time scale factor a.

 

The EMB translation transformation features in the validity scope are equivalent to the classical Galileo transformation features (with the scale change).

 

No relativistic effects exist in this case. The transformation with validity scope limited to the plane cannot be use in physics.  We know that the inverse transformation (5) in 3D space is not identical with the EMB text (EMB7) and (EMB8).  The coordinate transformation symmetry is missing in the EMB transformation validity scope.

4           Conclusions

The physical use of EMB transformations is based on the idea of the orthogonal coordinate systems, on idea that the x and t axes are the distance and time axes respectively, all scales are the same, the transformation is valid at any point of the space and physical effects are invariant with regard to the transformation.  The physical use is based on the idea that the origin of the moving coordinate system is translated from the stationary one (the translation is time dependent with constant velocity).

The interpretation of the transformation where there are two sloping space-time x andt axes and where the position of the axes is dependent on the “moving” coordinate system velocity does not give any sense in physics. Moreover the transformation does not translate the coordinate system origins. The “moving” coordinate system has its origin at the same place as stationary one.  But this variant does not change scales and inverse transformation is symmetric and equal to EMB text.

The EMB transformation has orthogonal axes and origin translation only in classical 3D space.  This interpretation of the EMB transformation is mathematically valid only in the moving plane.  But the transformation changes scale in one axis and inverse transformation differs from EMB text in this case. No relativistic effect exists in the validity scope.

 

We can resume. No interpretation of the EMB transformation can be used in physics. There is no possibility how to fulfil all required physical features of the transformation in one variant of the interpretation.

 

It is useless to try to experimentally prove the special relativity theory described in the EMB text.  It can not be successful. It can be only a game with words.

It is better to focus scientific effort to humility measurement in very different experiments. It is better to try to find a different interpretation of the experimental results. It is possible to discover new undiscovered and maybe quite surprising effects and new physical laws describing the world more exactly.

It would be very interesting to explain every experiment interpreted as a proof of the special relativity theory with respect of the EMB text analysis result. It is possible, that some of them can open the way to undiscovered physical law.

The EMB text influenced thinking of several generations of physicists. It would burden their minds and their physical imagination for next several years. It is the time to change the status and open a new space for a new discovery.

The conclusion does not decrease other very important contribution of A. Einstein to modern physics.

5           Original Quotes

Page 41, §2. On the Relativity of Lengths and Times

 

(EMB1)

The following reflexions are based on the principle of relativity and on the principle of constancy of the velocity of light. These two principles we define as follows:-

…                                                                                                                             

2. Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body.

 

Page 43, §3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former

 

(EMB2)

Let us in “stationary” space take two systems of co-ordinates, i.e. two systems, each of three rigid material lines, perpendicular to one another, and issuing from a point. Let the axes of X of the two systems coincide, and their axes of Y and Z respectively be parallel. Let each system be provided with a rigid measuring-rod and a number of clocks, and let the two measuring-rods, and likewise all the clocks of the two systems, be in all respects alike.

Now to the origin of one of the two systems (k) let a constant velocity v be imparted in the direction of the increasing x of the other stationary system (K), and let this velocity be communicated to the axes of the co-ordinates, the relevant measuring-rod, and the clocks. To any time of the stationary system K there then will correspond a definite position of the axes of moving system, and from reasons of symmetry we are entitled to assume that the motion of k may be such that the axes of moving systems are at time t (this “t” always denotes a time of stationary system) parallel to the axes of stationary system.

We now imagine space to be measured from stationary system K by means of the stationary measuring–rod, and also from the moving system k by means of measuring-rod moving with it; and that we thus obtain the co-ordinates x,y,z and  x,h,z respectively. Further, let us the time t of the stationary system be determined for all points thereof at which there are clocks by means of light signals in the manner indicated in §1; similarly let the time t of the moving system be determined for all points of the moving system at which there are clocks at rest relatively to that system by applying the method, given in §1, of light signals between the points at which the latter clocks are located.

 

Pages 43+44, §3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former

 

(EMB3)

To any system of value x,y,z,t, which completely defines the place and time of an event in stationary system, there belongs a system of values x,h,z,t determining that event relatively to the system k, and our task is now to find system of equations connecting these quantities.

 

Page 44, §3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former

 

(EMB4)

 

Page 46, §3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former

 

(EMB5)

 

Page 46, §3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former

 

(EMB6)

 

Page 47, §3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former

 

(EMB7)

 

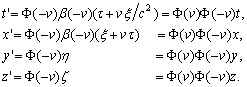
Page 48, §3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former

 

(EMB8)

 

Page 48, §3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former

 

(EMB9)

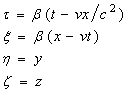
where

 

Page 48, §4. Physical Meaning of the Equations Obtained in Respect to Moving Rigid Bodies and Moving Clocks

(EMB10)

 

Page 48, §4. Physical Meaning of the Equations Obtained in Respect to Moving Rigid Bodies and Moving Clocks

 

(EMB11)

…at the time t=0 is

 

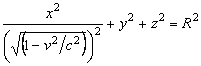
Page 48, §4. Physical Meaning of the Equations Obtained in Respect to Moving Rigid Bodies and Moving Clocks

 

(EMB12)

A rigid body which, measured in a state of rest, has the form of a sphere, therefore has in a state of motion – viewed from the stationary system – the form of an ellipsoid of revolution with the axes

 

Page 49, §4. Physical Meaning of the Equations Obtained in Respect to Moving Rigid Bodies and Moving Clocks

 

(EMB13)

Page 50, §5. The Composition of Velocities

 

(EMB14)

 

Page 50, §5. The Composition of Velocities

 

(EMB15)

 

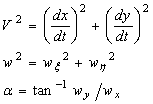
Page 51, §5. The Composition of Velocities

 

(EMB16)

It follows from this equation that from a composition of two velocities which are less than c, there always results a velocity less than c.

                                                                                                                                

 

Page 51, §5. The Composition of Velocities

 

(EMB17)

It follows, further, that the velocity of light c cannot be altered by composition with a velocity less than that of light. For this case we obtain

 

References

[1] Einstein A 1905 On the Electrodynamics of Moving Bodies – translated from „Zur Elektrodynamik betwegter Körper“ , Annalen der Physik, 17,1905 - The Principle of Realitvity – A Collection of Original Memories on the Special and General Theory of Relativity – Mineola, N.Y.: Dover Publication 1952, pages 35-65.

 

[2] Einstein A 1916 The Foundation of the General Theory of Relativity – translated from „Die Grundlage der allgemeinen Relativitätstheorie“, Annalen der Physik, 49,1916 - The Principle of Realitvity – A Collection of Original Memories on the Special and General Theory of Relativity - Mineola, N.Y.: Dover Publication 1952, pages 109-164.

 

[3] Pavlovic M R 2004 Einstein's Theory of Relativity - Scientific Theory or Illusion?, [Online], Available: http://www.geocities.com/milanrpavlovic/ [20 Mar 2005]

 

[4] Galeczki G 2005 Special Relativity’s Heel of Achilles: The Units of Measurements, [Online], Available: http://www.helmut-hille.de/units.html [20 Mar 2005]

 

[5] Hille H 2005 Does the Michelson Experiment call for a Relativistic Explanation?

A question posed to the reader, [Online], Available: http://www.helmut-hille.de/michelson-e.html [20 Mar 2005]

 

[6] Hafele J C and Keating R E 1972 Around-the-World Atomic Clocks: Predicted Relativistic Time Gains Science, Volume 177, July 14, 1972, pages 166-170.

 

[7] California Institute of Technology, Massachusetts Institute of Technology 2005 LIGO –  Laser Interferometer Gravitational Wave Observatory, [Online], Available: http://www.ligo.caltech.edu/ [4 Dec 2005]

 

[8] Neumann L 2005 Gravity Dynamics and Gravity Noise on the Earth Surface, Preprint [Online], Available: http://www.dynamicgravity.org/p1/doc/ [24 Jan 2005]

 

[9] André Angot 1971 Užitá matematika pro elektrotechnické inženýry - translation of „Compléments de Mathématiques ‚a ¾usage des Ingénieurs de ¾Electrotechnique at des Télécommunications, MASSON at Cie (Editions de la Revue ïOptique, Paris, 1952), Praha : SNTL

 

[10]MATHWORLD 2005 Algebra, Calculus and Analysis, [Online], Available:  http://mathworld.wolfram.com/ [28 Sep 2005]

 

[11] TEMPLE University 2005 Review of Linear Algebra, [Online], Available: http://courses.temple.edu/economics/notes/algebra/NBUCK1.htm [15 Aug 2005]

 

[12] Dictionary on Labor Law Talk 2005 Authomorphism, [Online], Available: http://encyclopedia.laborlawtalk.com/Automorphism [27 Sep 2005]

 

 

[13] Wondratschek H 2002 Matrices, Mappings, and Crystallographic Symmetry, International Union of Crystallography, [Online], Available: http://journals.iucr.org/iucr-top/comm/cteach/pamphlets/22/22.html [26 Nov 2005], pages 66-70.

 

[14] Wikipedia 2005 Translation (geometry), [Online], Available: http://en.wikipedia.org/wiki/Translation_%28geometry%29 [11 Dec 2005]

 

 [15]Young-Hoo Kwon 1998 Mechanical Basis of Motion Analysis - Transformation Matrix, [Online], Available: http://kwon3d.com/theory/transform/transform.html [26 Nov 2005]